les espaces de Calibi-yau

 

 

Qu'est-ce ?

Un espace de plus de quatre dimensions,

produit de la géométrie algébrique.

Quand la science rejoint l'art

et crée la beauté des chiffres.

voir : https://www.google.com/search?q=espace+de+calabi+yau&client=firefox-b-d&tbm=isch&source=iu&ictx=1&fir=gSC4uFZCKN5GBM%252CnFlBVTpOppRA1M%252C%252Fm%252F019vl3&vet=1&usg=AI4_-kTJuHaoXHoIW6uVdGtgunboqI_SNQ&sa=X&ved=2ahUKEwiaoOfyiaDwAhXyEWMBHe_rA_4Q_B16BAggEAE#imgrc=gSC4uFZCKN5GBM

Le zéro

Le zéro est-il un nombre ? Peut-on dire que rien est un nombre à l’égal du un ou deux cent ou mille ?

Ce rien qui représente malgré tout quelque chose fut inventé il y a mille huit cent ans en Inde. Le mathématicien Brahmagupta dans son livre intitulé Le commencement de l’univers définit le zéro : « Le zéro est le résultat de la soustraction d’un nombre de lui-même ». A son époque, si l’on retirait deux pommes de deux pommes il n’y avait pas de résultat. Brahmagupta donna un nom à ce rien, le zéro et afirma que ce nom est un nombre et non rien. Il écrivit ainsi la règle : « Quand zéro est ajouté à un nombre ou soustrait d’un nombre, ce nombre reste inchangé » et il ajouta « le produit d’un nombre multiplié par zéro est zéro ».

Est-ce si évident ? Pourquoi pour l’addition ou la soustraction par zéro, le nombre multiplié ou soustrait reste le même et pourquoi lorsqu’il s’agit de multiplication ou division ce nombre devient égal à zéro ? Que dire alors de zéro divisé par zéro ? Il n’y a pas de réponse ou plutôt la réponse est indéterminée.

La règle jusqu’au XVII° siècle faisait commencer les séries de chiffres par un (puis deux, trois, etc.). C’est ainsi que l’an zéro n’existe pas dans le calendrier grégorien qui passe de 1 av. J-C à 1 ap. J-C sans transition. Cette anecdote fut difficile à juguler lors du passage à l’an 2000. C’est pour cela que le deuxième millénaire a commencé en l’an 2001 qui et réellement éloigné de deux mille ans de la naissance du Christ.

Le zéro est donc un nombre au même titre que les autres nombres, même si son destin est particulier.

Illogisme de la logique

C’est le mathématicien Gödel qui démontra que la logique contient toujours de l’illogisme. Tout système logique est incomplet en lui-même, car il existe toujours des propositions indécidables dans tout système arithmétique, c’est-à-dire des énoncés mathématiques dont on ne peut jamais dire s’ils sont vrais ou faux. Tout système est incomplet en lui-même. Il faut lui ajouter des axiomes supplémentaires extérieurs à lui pour qu’il soit cohérent.

Ainsi des failles logiques se manifestent dès qu’on aborde des propositions autoréférentielles, c’est-à-dire qui font référence à elle-même. Deux exemples :

« La présente phrase est fausse. » Si la phrase est vraie, elle est fausse ; si elle est fausse, elle est vraie. La logique se contredit.

« Un habitant de Séville est rasé par le barbier de Séville si et seulement s’il ne se rase pas lui-même. Alors, est-ce que le barbier de Séville se rase lui-même ? » S’il se rase lui-même, il ne peut être rasé que par le barbier de Séville, donc il ne se rase pas lui-même ; mais s’il ne se rase pas lui-même, il est rasé par le barbier de Séville, donc il se rase lui-même.

Ces deux exemples sont tirés du livre de Trinh Xuan Thuan, Le chaos et l’harmonie, la fabrication du Réel, Arthème Fayard, 1998. Sa conclusion : l’univers est conscient de lui-même et le fait que l’homme ne subisse pas aveuglément  les lois de la nature sans les comprendre est porteur de signification. Nous avons le don de comprendre parce que l’Univers n’est pas qu’une collection de particules de matière inerte. Il est la manifestation d’un principe infiniment plus subtile et élégant. L’univers a un sens, et c’est l’homme qui, en le comprenant, lui confère ce sens.

Mais la science ne pourra jamais aller au bout du chemin par les mathématiques. Il faut à l’homme d’autres outils et d’autres modes de connaissance pour le comprendre, telle l’intuition mystique.

Zéro

Est-ce un chiffre ?
Est-ce un concept ou un mirage ?
Il est attirant, comme l’hypnose.
On se concentre dessus et on flotte.
Rien ne peut vous occuper autant l’esprit
Que ce Zéro qui est sans exister.

Indiquer qu’il n’est rien, est-ce une solution ?
Cela peut, mais Zéro, virgule, quelque chose
Qu’est-ce ? Un souffle d’inepties.
S’il y a quelque chose, c’est forcément Un.
Peut-il y avoir moins que Un ?
S’il n’y a pas Un, il y a Zéro, c’est-à-dire rien.
Il y a soit une chose, soit son contraire,
Mais pas les deux qui feraient trois.
Supposons qu’entre le Un et le Zéro,
Il y ait la moitié d’un Un.
C’est bien une chose en soi cette moitié !
C’est donc bien un Un appartenant à un Deux.
Toute chose divisible fabrique une autre chose
Qui est pleine et entière, donc Un
Et ce Un appartient bien à un autre Un
Pour former un Deux plein et entier
Le Un devient alors Trois et ce nouveau chiffre
Est un ensemble qui forme un autre Un
Différent de tous les Uns existant.

Ah, quelle migraine !

On peut additionner le Zéro à un Un
Voire Deux ou mille
Cela donne un, deux ou mille.
Mais Un plus Zéro égale Un,
Et Un plus Un plus Zéro égale deux,
Alors que Un multiplié par Zéro égale Zéro.
Quant à Un divisé par Zéro, n’en parlons pas,
C’est un néant inimaginable !

Mais revenons à 0,5 ?
Est-ce quelque chose que cette moitié de chose ?
Soit cela n’existe pas, et c’est bien Zéro ;
Soit cela est, et c’est Un, puisqu’il existe.
Compter, c’est commencer par Un,
Puis deux, puis trois, puis mille,
Jusqu’à un Infini inimaginable
Qui ne forme qu’un Un pour le Créateur.
Lui-même est un autre Un,
Et ces deux Un ne font pas deux,
Ils font même plus que l’Infini.
Ils sont Tout, comprenant le Rien qui n’existe
Que parce qu’il y a au moins un Un.

Dieu, quelle migraine multipliée !

Et que dire lorsqu’on pense aux contraires
Moins Un est-il le pendant de Un ?
Peut-il y avoir moins quelque chose
Qui fasse un quelque chose inversé ?
Le Zéro n’est alors qu’un col ou un canyon
Qui permet à la nature
D’assouvir sa soif d’exister.
Si je ne suis pas, je suis malgré tout.
Si l’infini est là, y a-t-il un autre infini
Qu’on ne peut saisir ou imaginer ?
Quand je pense qu’il y a un moi-même
Qui me regarde et me juge et rit
Et s’amuse de ces incompréhensions.
Qu’est-il pour se moquer ainsi ?

Oui, c’est faux. De vrais maux de tête !

Il est trois heures.
Tient, là aussi, quelle bizarrerie !
Trois heures, c’est une heure dans la nuit,
Une seule. Il n’y a pas deux trois heures.
Et pourtant on n’écrit pas trois heure.
On ajoute un s à heure parce qu’il y en a plusieurs.
Mais plusieurs quoi ? Plusieurs heures
Ou une seule trois heures ?
Trois heure (s) est bien seule,
Mais elle est trois.

Ce n’est plus la migraine,
Mais l’anéantissement…

Dormons !

©  Loup Francart

La Déesse des petites victoires, roman de Yannick Grannec

Un livre étrange où l’on passe de la plus haute mathématique aux soins d’une vieille dame à l’humeur inégale. Les premières pages (au moins une bonne cinquantaine) laissent le lecteur dérouté. 1980, à Princeton : première rencontre entre Anna Roth, une jeune documentaliste et Adèle Gödel, femme du mathématicien Kurt Gödel, ami d’Einstein. La première est chargée de récupérer les archives que détient la seconde. Pour y arriver, elle devra devenir l’amie d’Adèle, petite femme coriace, au destin particulier : elle a veillé toute sa vie sur un des plus grands mathématiciens du siècle qui se comporte comme un enfant sans jugeote. Deuxième chapitre : Adèle, une jeune serveuse de bar, fait connaissance avec Kurt Gödel, un jeune homme au comportement bizarre qui réfléchit en marchant la nuit dans les rues de Vienne. Kurt et moi n’avions rien en commun, du moins si peu. J’avais sept ans de plus, je n’avais pas fait d’études ; il préparait son doctorat. (…) La promenade s’est achevée comme elle avait commencé, dans le très inconfortable silence où chacun cachait ses pensées. Même si je n’ai jamais été douée pour les mathématiques, je connais ce postulat : une toute petite inflexion de l’angle de départ fait une énorme différence à l’arrivée. Dans quelle dimension, quelle version de notre histoire, ne m’a-t-il pas raccompagnée ce soir-là ?

On ne comprend que plus loin que le livre s’organise entre la vraie vie d’Adèle et de Kurt (Vienne, fuite devant l’Allemagne nazie, installation aux Etats-Unis) et la vie d’Adèle devenue vieille, phagocytant la vie d’Anna, missionnée auprès d’elle pour obtenir le nachlass de Kurt (documents faisant figure d’héritage intellectuel recueillis de manière posthume). Un chapitre dans les années suivant la deuxième guerre mondiale, un chapitre dans les années 80.

Les mathématiciens sont comme des enfants qui empilent des briques de vérité les unes sur les autres pour construire le mur qui remplira le vide de l’espace. Ils se demandent si certaines sont vraiment solides, si elles ne vont pas s’écrouler ensemble. J’ai prouvé que sur une certaine partie du mur, certaines briques sont inaccessibles. On ne pourra donc jamais vérifier que tout le mur est solide. C’est ainsi que Kurt explique son travail sur le programme de Kilbert, liste de questions dont il a résolu une partie avec son théorème d’incomplétude prouvant que certaines résolutions étaient inaccessibles. Pour Kurt, les mathématiques sont la vraie beauté. Il s’interroge sur l’existence de l’infini. Il explique la théorie des ensembles à Adèle qui lui demandait si l’on invente les mathématiques ou si on les découvre. Et il ajoute : « Je cherche à établir la décidabilité de l’hypothèse du continu. (…) J’ai l’intuition, Adèle, que l’hypothèse du continu est fausse. Il nous manque des axiomes pour construire une définition correcte de l’infini. (…) Je dois savoir si cet infini que j’explore est une réalité ou une décision. Je veux témoigner de notre avancée dans un univers de plus en plus lisible. Je dois découvrir si Dieu a créé les nombres entiers et l’homme, et le reste. »

Mais Adèle est perdue devant ces réflexions : Je retournais à ma cuisine. Les larmes avaient monté malgré moi ; ils devaient me croire inquiète pour l’avenir de l’humanité, en réalité, je m’apitoyais sur mon sort. J’étais une enfant dans un monde d’adultes. (…) Je ne serais jamais d’ici ; je serais toujours une exilée au milieu de tous ces génies. J’atteignais l’âge où les hommes seraient plus charmés par ma cuisine que par mes jambes : l’âge de la résignation.

Kurt finit par mourir. Est-il décédé de malnutrition comme ils l’ont dit ? Non, plutôt d’un accident du travail : il interrogeait l’incertitude ; il était mort rongé par le doute. La vie n’est pas une science exacte ; tout y est fluctuant, indémontrable. Il ne pouvait la vérifier paramètre par paramètre. Il ne pouvait pas axiomiser l’existence.  Qu’avait-il cherché qui n’était pas dans son cœur, son ventre ou son sexe ? Il avait décidé de ne pas s’impliquer ; de se placer en dehors du monde pour le comprendre. Il y a des systèmes dont on ne peut s’exclure. Albert (Einstein) le savait, lui. S’exclure de la vie, c’est mourir.

Oui, un livre qui passe des plus hautes réflexions sur l’univers aux plus ordinaires sentiments d’une vieille femme qui s’accroche à son destin. Et pourtant : Je n’existais pas pour eux. Je n’ai jamais existé.

Pavage de Penrose

 

Penrose est un mathématicien  et physicien britannique qui a largement contribué à l’élaboration de la théorie de la relativité générale pour ce qui concerne la cosmologie et l’étude des trous noirs.

Il est connu pour sa découverte en 1974 de pavages constitués de deux formes et permettant de couvrir en entier un plan de manière non périodique. Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle de 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement.

 

 

Le pavage de type 0 se construit avec des triangles d’or (voir le nombre d’or, publié le 14 février). En découpant un premier triangle d'or (aigu ou obtus, peu importe) et en opérant un agrandissement d'un facteur φ, puis en recommençant l'opération précédente une infinité de fois, on constitue un pavage complet du plan à l'aide des deux types de triangles d'or. On peut donc paver des triangles d’or par des triangles d’or.

 

 

 

 

 

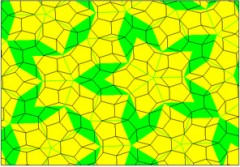
 Le pavage de type 1 permet de couvrir un plan avec des pentagones en ajoutant trois pièces qui permettent de combler les trous. Ce sont un losange, un pentagramme et un bateau.

 

 

 

 

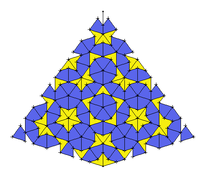
  Le pavage de type 2 est constitué de cerfs-volants et de fléchettes, construits à partir de triangles d’or. Cela ne permet de générer qu’un seul type de pavage. Il est facile de prouver que, comme pour les triangles d'or, la proportion entre le nombre de cerfs-volants et celui de fléchettes tend vers le nombre d'or φ, ce qui assure que le pavage ainsi construit n'est pas périodique.

 

  

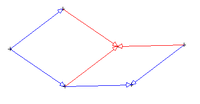
Le pavage de type 3 permet de paver le plan à l'aide de deux figures géométriques simples comme les deux losanges suivants.

Ce qui donne :

 

 

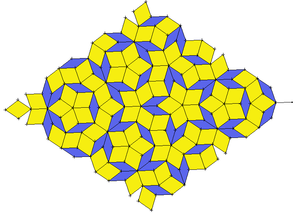
Penrose a rendu le rêve mathématique. L'imagination peut peupler le monde réel de figures ordonnées, mais d'une symétrie particulière. Quelles belles fleurs dans le jardin de l'univers !