Pavage de Penrose

 

Penrose est un mathématicien  et physicien britannique qui a largement contribué à l’élaboration de la théorie de la relativité générale pour ce qui concerne la cosmologie et l’étude des trous noirs.

Il est connu pour sa découverte en 1974 de pavages constitués de deux formes et permettant de couvrir en entier un plan de manière non périodique. Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle de 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement.

 

 

Le pavage de type 0 se construit avec des triangles d’or (voir le nombre d’or, publié le 14 février). En découpant un premier triangle d'or (aigu ou obtus, peu importe) et en opérant un agrandissement d'un facteur φ, puis en recommençant l'opération précédente une infinité de fois, on constitue un pavage complet du plan à l'aide des deux types de triangles d'or. On peut donc paver des triangles d’or par des triangles d’or.

 

 

 

 

 

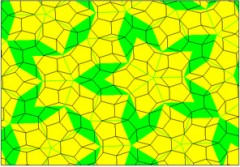
 Le pavage de type 1 permet de couvrir un plan avec des pentagones en ajoutant trois pièces qui permettent de combler les trous. Ce sont un losange, un pentagramme et un bateau.

 

 

 

 

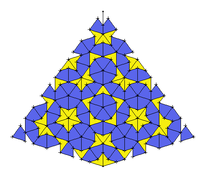
  Le pavage de type 2 est constitué de cerfs-volants et de fléchettes, construits à partir de triangles d’or. Cela ne permet de générer qu’un seul type de pavage. Il est facile de prouver que, comme pour les triangles d'or, la proportion entre le nombre de cerfs-volants et celui de fléchettes tend vers le nombre d'or φ, ce qui assure que le pavage ainsi construit n'est pas périodique.

 

  

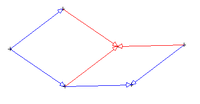
Le pavage de type 3 permet de paver le plan à l'aide de deux figures géométriques simples comme les deux losanges suivants.

Ce qui donne :

 

 

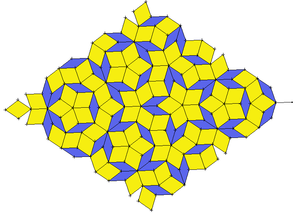
Penrose a rendu le rêve mathématique. L'imagination peut peupler le monde réel de figures ordonnées, mais d'une symétrie particulière. Quelles belles fleurs dans le jardin de l'univers !