L'infini

Le silence éternel de ces espaces infinis me terrifie. (Pascal)

 

Un simple mot, infini, qui ouvre toutes grandes les portes de l’inconnaissance. Le mot existe, mais qu’est-il, comment le définir, que représente-t-il ? C’est une énigme, un mystère même qui reste éternel, même pour ceux qui travaillent sur le concept. Ce n’est plus un nombre, car chaque nombre correspond à une suite de nombres, mais il est utilisé dans de nombreux calculs. Il est plus qu’un concept scientifique. Il a également une signification mystique et religieuse. Mais qu’englobe-t-il ?

Il est possible que je me trompe, mais je pense qu’il englobe l’ensemble du monde visible et invisible envisageable par l’homme. Il s’agit en premier lieu du monde matériel, du plus petit morceau d’atome à l’univers dans sa totalité qui est encore inconnu, mais que l’on commence à cerner puisqu’on en connait la date de naissance, 13,8 milliards d'années.

Le mathématicien Georg Cantor, créateur de la théorie des ensembles, a démontré ce qui apparaît aujourd’hui comme une évidence (hum !), à savoir que le tout est plus grand que la somme de ses parties ou encore que les nombres algébriques peuvent être numérotés, ce qui n’est pas le cas des nombres réels. Ce que montre Cantor, c’est que, une fois franchie la barrière conceptuelle qui rendait l’infini inaccessible, alors rien ne s’oppose à développer une arithmétique des nombres infinis — ou, plutôt, transfinis, c’est-à-dire au-delà du fini, ou encore ordinaux.

Mais il s’agit également de ce que Pierre Teilhard de Chardin appelait la noosphère, qui englobe la terre ou même probablement l’univers, c’est-à-dire le monde de la pensée, immatériel, mais qui existe bien sûr et ne peut être nié. C’est certes une production de notre cerveau matériel, mais elle s’est créée en cours de route du devenir de l’univers et a pris son indépendance. La noosphère serait-elle cette partie du tout qui dépasse la somme des parties ?

Autre bizarrerie. On peut concevoir l’infini de deux manières. La première le voit comme un point qui s’éloigne en permanence quand on avance vers lui. C’est le paradoxe d’Achille et de la tortue. La seconde l’imagine comme une ouverture toujours plus grande qui ne peut avoir de fin, car plus on approche, plus elle s’ouvre. On retrouve le même constat dans la noosphère et le monde conceptuel. On peut imaginer un infiniment concevable. L’aventure de la pensée ne cesse de progresser et progressera en permanence parce que ce qu’il y a à découvrir est infini. Mais il est également possible de le voir comme un infiniment inconcevable parce que les concepts ne sont que des choses finies et que ceux-ci ne sont que des constructions à partir du non fini. Plus le concevable s’enrichit, plus l’inconcevable augmente.

Enfin, la notion d’infini s’entend également de manière théologique. Tout infini n’est qu’une réalité potentielle puisque, dit Aristote, « l’infini est ce qui est tel que lorsqu’on en prend une quantité, c’est-à-dire quelque grande que soit la quantité qu’on prend, il reste toujours quelque chose à prendre ». Jean Duns Scot transforme cet axiome en énonçant que l’infini n’est pas ce qui laisse toujours quelque chose derrière, mais bien ce qui excède le fini selon toute proportion déterminée ou déterminable. Pour lui, seul Dieu est infini.

Le monde divin reste une énigme, c’est-à-dire une certitude pour les uns ou une chimère pour les autres. De nos jours, le concept d’infini ne semble pas inclure ce monde qui, pour l’instant, reste indémontrable. Mais, est-ce vrai ? Tous les mathématiciens et cosmologues qui se sont penchés sur ce problème incluent plus ou moins ouvertement la notion de Dieu comme étant le seul véritable infini. Certes, il ne s’agit plus du Dieu des religions, mais d’un au-delà de la création, existant à côté de celle-ci ou au sein de celle-ci.

Dieu… transcendant et/ou immanent… ou autre encore…

Mais peut-on parler de Dieu tel que l’imaginent les hommes ?

L'ensemble de Mandelbrot

L’ensemble de Mandelbrot c’est en premier lieu un dessin généré par un ordinateur. C’est une collection de points. Celle-ci contient des aires, mais également des courbes lisses, des filaments, des points d’où émanent de multiples branches, et d’autres choses.

L'ensemble de Mandelbrot tire ses origines de la dynamique complexe, un domaine défriché par les mathématiciens français Pierre Fatou et Gaston Julia au début du XXe siècle. La première représentation de cet ensemble apparaît en 1978 dans un article de Robert Brooks et Peter Matelski. Le 1er mars 1980, au centre de recherche IBM Thomas J. Watson (dans l'État de New York), Benoit Mandelbrot obtient pour la première fois, une visualisation par ordinateur de cet ensemble. En 1984, l'étude de l'ensemble de Mandelbrot commence réellement avec les travaux d'Adrien Douady et John H. Hubbard, qui établissent ses propriétés fondamentales et baptisent l'ensemble en l'honneur de Mandelbrot. (…) Dans le numéro d'août 1985 du magazine Scientific American l'ensemble de Mandelbrot est présenté au grand public comme « l'objet mathématique le plus complexe jamais découvert » et présente l'algorithme qui permet de le tracer soi-même. (http://fr.wikipedia.org/wiki/Ensemble_de_Mandelbrot)

Que représente l’ensemble de Mandelbrot ? En gros à chaque point de l’image correspond un système dynamique sous-jacent. Le point joue le rôle d’un paramètre ajustable. Différents points correspondent à des ensembles de Julia différents, à des systèmes différents, et selon le comportement de ces derniers, on peut décider de colorier le point de telle ou telle façon. L’ensemble de Mandelbrot est l’ensemble des paramètres pour lesquels le système a une certaine propriété (l’ensemble de Julia est en un seul morceau). D’où son surnom de Chef d’orchestre.

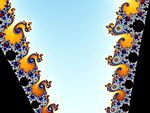
Voici Trois exemples de représentations de l’ensemble de Mandelbrot. Les images montrent des détails de l’ensemble, mis en relief de diverses façons, au sens propre comme au sens figuré :

L'ensemble de Mandelbrot doit beaucoup sa popularité à la variété et la beauté de ses structures et à la profondeur infinie de ses détails, mais aussi à la possibilité de l'explorer soi-même à l'aide des nombreux logiciels aujourd'hui disponibles.

La séquence d'exploration commentée ci-dessous est un zoom profond vers la valeur de c = -0,743643887037151 + 0,13182590420533i, à travers nombre de motifs caractéristiques. Le rapport de grossissement entre la dernière et la première image est d'environ 60 milliards.

Étape	Description
	L'ensemble de Mandelbrot initial. Si la dernière image était en taille réelle, cet ensemble de Mandelbrot aurait une taille de 3 millions de kilomètres et sa frontière présenterait une quantité astronomique de structures fractales. Nous allons zoomer sur la vallée située entre la cardioïde et le bourgeon principal.
	Cette vallée a été baptisée « vallée des hippocampes ».
	À gauche, des spirales doubles, à droite les « hippocampes ». Nous zoomons sur l'un d'eux.
	Un « hippocampe », tête en bas. Cet hippocampe est composé de 25 « antennes » consistant en 2 groupes de 12 et un filament relié à la cardioïde. Nous en déduisons que le bourgeon qui le porte a une périodicité de 25. Le point de rencontre de ces antennes est un « point de Misiurewicz ». Sur la plus longue antenne, celle qui mène à la « queue » de l'hippocampe, on reconnaît une copie réduite de l'ensemble de Mandelbrot, appelée aussi « satellite ».

 Et voici ce que cela donne :

La science et l'art se rejoignent dans cette œuvre fantastique, simple et belle.

Merci Monsieur Mandelbrot !

Amusement sur les pavages de Penrose

 Source : http://serge.mehl.free.fr/chrono/Penrose.html

Éminent physicien et mathématicien, Roger Penrose est diplômé de l'université de Cambridge. Sa thèse (1958) porte sur les méthodes tensorielles en géométrie algébrique.

Entre 1964 et 1973, il enseigne les mathématiques au Birkbeck College de Londres et rencontre le célèbre physicien Stephen W. Hawking, son compatriote, à qui l'on doit un célèbre ouvrage : Une brève histoire du temps, Trous noirs et bébés univers.

Ils travaillèrent ensemble sur une théorie de l'origine de l'univers. C'est ainsi que Penrose apporta sa contribution mathématique à la théorie de la relativité générale appliquée à la cosmologie et à l'étude des trous noirs. Professeur à Oxford, il reçut, avec Hawking, le prix Wolf 1988 pour la physique et fut anobli par la reine d'Angleterre en 1994.

Contrairement à une conjecture que l'on croyait bien assise, à savoir que tout pavage du plan peut se ramener à un pavage périodique, Penrose montra (1974) que l'on peut obtenir un pavage non périodique en faisant usage de ces deux seuls types de "tommettes" judicieusement placées, faisant d'ailleurs apparaître deux types de décagones, éventuellement imbriqués, comportant chacun 5 pavés de losanges fabriqués à partir de deux triangles isocèles obtus et 5 pavés de losanges fabriqués à partir de deux triangles isocèles aigus.

 

Surgi de l’univers, cet ensemble trace sa route vers les humains, comme pour leur dire : "Oui, l’univers est organisé, intelligent et divin ! "

 

Les incertitudes de la science

 

« La cible privilégiée de René Thom, ce sont tous les savants qui, à la manière de Prigogine, nous expliquent que le monde n’est que bruits et hasards : la « prétendue science du chaos ».

Prigogine, selon Thom, a amalgamé dans une science du chaos des phénomènes essentiellement différents, dont relèvent du déterminisme et d’autres de la description probabiliste. Thom reprend l’exemple de la pièce de monnaie cher à Prigogine : Prigogine nous a expliqué qu’il est par définition impossible de prévoir si une pièce lancée en l’air retombera sur pile ou sur face, et que la seule détermination est d’ordre statique. Cette image d’incertitude et de probabilité résumerait assez bien, selon Prigogine, l’état actuel de la science contemporaine. Mais, me dit Thom, Prigogine nous abuse : si les physiciens ne peuvent pas prévoir le mouvement de la pièce, ce n’est pas parce que c’est impossible, mais parce que c’est expérimentalement difficile et coûteux. Cette prévision reste théoriquement possible pour un observateur qui contrôlerait les conditions initiales du jet de manière assez précise. »

Guy Sorman, Les vrais penseurs de notre temps, Fayard, 1989, p.61

 

René Thom, mathématicien français (1923-2002), n’était pas que mathématicien. Il s’intéressait également à la philosophie. C’est cette alliance entre les mathématiques et la philosophie qui lui font dire que la théorie du hasard et du chaos n’est qu’une mode intellectuelle. Prétendre que la matière ou la vie sont les produits du hasard, c’est se glorifier de son incompréhension, accepter que le monde ne soit pas intelligible.

Bref, Thom pense qu’il faut retrouver Aristote et rapprocher le quantitatif du qualitatif, le sensible et l’intelligible, la science et la conscience.

Le génie est moins dans la science des mesures que dans une science herméneutique : l’interprétation des signes par les mathématiques.

Les canons de l'Offrande musicale

L’offrande musicale est un des chefs d’œuvre de Bach. Il a conçu les canons comme de véritables rébus musicaux qui font également penser aux gravures de Escher, à la géométrie et plus particulièrement aux symétries diverses. Le canon en crabe en est un exemple. Il constitue un palindrome musical, figure de style désignant un mot, ou même un texte, qui peut être lu à l’endroit et à l’envers (exemple : ressasser).

http://www.youtube.com/watch?v=4VFJdMRg_Yo

 

Le manuscrit de Bach peut être joué dans les deux sens, du début à la fin ou de la fin au début. Mieux, il se décompose à deux voix dans de nombreuses dimensions qui vont jusqu’à former un ruban de Mobius.

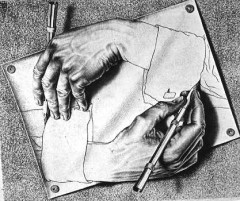
N’est-ce pas génial cette complicité inventive dans des domaines différents qui se rejoignent : littérature, dessin, musique, mathématique. Et tout cela à partir de différentes formes de symétrie, comme un miroir enchanté qui vous aide à rêver.

 

Alors, écoutons et regardons...

 

Le nombre d'or

 

Première partie d'une recherche qui conduit à créer des dessins géométriques aux formes bizarres et parfois non périodiques, c'est-à-dire sans reconduction par imitation d'un élément de figure sur l'autre.

Ouvrez le fichier :

Le nombre d'or.doc

 

Nous verrons comment certains mathématiciens se sont intéressés au dessin géométrique et ce qu'ils en ont tiré, en particulier Penrose qui a inventé ses pavages non périodiques.