L'ensemble de Mandelbrot

L’ensemble de Mandelbrot c’est en premier lieu un dessin généré par un ordinateur. C’est une collection de points. Celle-ci contient des aires, mais également des courbes lisses, des filaments, des points d’où émanent de multiples branches, et d’autres choses.

L'ensemble de Mandelbrot tire ses origines de la dynamique complexe, un domaine défriché par les mathématiciens français Pierre Fatou et Gaston Julia au début du XXe siècle. La première représentation de cet ensemble apparaît en 1978 dans un article de Robert Brooks et Peter Matelski. Le 1er mars 1980, au centre de recherche IBM Thomas J. Watson (dans l'État de New York), Benoit Mandelbrot obtient pour la première fois, une visualisation par ordinateur de cet ensemble. En 1984, l'étude de l'ensemble de Mandelbrot commence réellement avec les travaux d'Adrien Douady et John H. Hubbard, qui établissent ses propriétés fondamentales et baptisent l'ensemble en l'honneur de Mandelbrot. (…) Dans le numéro d'août 1985 du magazine Scientific American l'ensemble de Mandelbrot est présenté au grand public comme « l'objet mathématique le plus complexe jamais découvert » et présente l'algorithme qui permet de le tracer soi-même. (http://fr.wikipedia.org/wiki/Ensemble_de_Mandelbrot)

Que représente l’ensemble de Mandelbrot ? En gros à chaque point de l’image correspond un système dynamique sous-jacent. Le point joue le rôle d’un paramètre ajustable. Différents points correspondent à des ensembles de Julia différents, à des systèmes différents, et selon le comportement de ces derniers, on peut décider de colorier le point de telle ou telle façon. L’ensemble de Mandelbrot est l’ensemble des paramètres pour lesquels le système a une certaine propriété (l’ensemble de Julia est en un seul morceau). D’où son surnom de Chef d’orchestre.

Voici Trois exemples de représentations de l’ensemble de Mandelbrot. Les images montrent des détails de l’ensemble, mis en relief de diverses façons, au sens propre comme au sens figuré :

L'ensemble de Mandelbrot doit beaucoup sa popularité à la variété et la beauté de ses structures et à la profondeur infinie de ses détails, mais aussi à la possibilité de l'explorer soi-même à l'aide des nombreux logiciels aujourd'hui disponibles.

La séquence d'exploration commentée ci-dessous est un zoom profond vers la valeur de c = -0,743643887037151 + 0,13182590420533i, à travers nombre de motifs caractéristiques. Le rapport de grossissement entre la dernière et la première image est d'environ 60 milliards.

Étape	Description
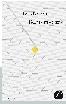
	L'ensemble de Mandelbrot initial. Si la dernière image était en taille réelle, cet ensemble de Mandelbrot aurait une taille de 3 millions de kilomètres et sa frontière présenterait une quantité astronomique de structures fractales. Nous allons zoomer sur la vallée située entre la cardioïde et le bourgeon principal.
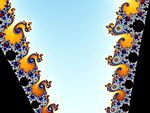
	Cette vallée a été baptisée « vallée des hippocampes ».
	À gauche, des spirales doubles, à droite les « hippocampes ». Nous zoomons sur l'un d'eux.
	Un « hippocampe », tête en bas. Cet hippocampe est composé de 25 « antennes » consistant en 2 groupes de 12 et un filament relié à la cardioïde. Nous en déduisons que le bourgeon qui le porte a une périodicité de 25. Le point de rencontre de ces antennes est un « point de Misiurewicz ». Sur la plus longue antenne, celle qui mène à la « queue » de l'hippocampe, on reconnaît une copie réduite de l'ensemble de Mandelbrot, appelée aussi « satellite ».

 Et voici ce que cela donne :

La science et l'art se rejoignent dans cette œuvre fantastique, simple et belle.

Merci Monsieur Mandelbrot !